DDPM

2024/9/16 读论文系列 Diffusion

论文发布日期：2020-12-16

发布会议/期刊：NeurIPS（CCF-A）

扩散模型太难了，论文看不懂，直接参考别人的写的原理笔记，省略了一些

扩散模型原理

背景知识

先验概率和后验概率
- 先验概率：根据以往经验和分析得到的概率，往往作为“由因求果“问题中的“因"出现，如
- 后验概率：指在得到“结果“的信息后重新修正的概率，是“执果寻因“问题中的“因"，如
贝叶斯公式
是先验概率，是后验概率，是证据，是似然，表示归因（证据）力度
高斯分布
表示均值，即期望。表示标准差

前向过程

前向过程是图片加噪的过程，将原图通道归一化后，取一张同样大小的高斯噪声图片相加迭代，得到

即：

其中，为了方便我们令，得到

现在思考一个问题，能否直接从到，直接避免中间的迭代过程，思考最后两步有

将下面的式子带入上面有

化简可得

现在我们可知

我们已知

因此

我们将原始得两个随机噪声可以合写为一个分布以上分布的噪声，得到

以此类推，可以得到

为方便表示，我们可以写成

反向过程

现在我们得到了一张不断加噪的图片，我们如何将这张图片重新还原成原图呢

我们先思考如何从还原为，通过贝叶斯公式我们可以得到

因为这些概率都是以为基准的，为了严谨，可以写成

我们现在来看右边三个概率

因为

所以三个概率满足下面三个分布

将它们写为高斯分布的概率密度函数形式可以得到

将这三个概率全部带入前面的贝叶斯公式可得

由此可知满足以下概率分布

我们的目标是利用和的关系，然后可以一直迭代到，因此要消去观察之前，我们已知

代入可得

至此就得到了与之间的概率关系

看上图我们可知在t较大的时候接近0，即我们可以认为任意一张高斯噪声图片都是某张原图加噪得来。那我们如何得到最初的图像呢，只要训练一个神经网络去预测噪声，然而随机采样不断迭代即可

优化目标

我们如何来预测噪声呢？

总的来说，在训练阶段，我们原本想推断条件分布，因为样本是已知的，因此可以通过后验分布来近似这个条件分布

神经网络就是学习后验分布进行训练，训练完毕后直接用来采样去预测噪声

我理解来讲就是，先给定图片和扩散次数，然后随机采样一个高斯噪声并保存好记作，接着根据加噪公式进行前向过程得到。神经网络的目标就是预测一个，通过损失函数约束使得这个接近的概率分布，最后不断进行反向过程生成，这个预测得到的就符合训练集的分布

训练的损失函数就是让神经网络近似后验分布，可以通过KL散度进行约束，即最小化两个联合分布的KL散度，得到

经过复杂的数学推导和重参数化技巧可以得到扩散模型的训练和采样算法，最终得到简化版：

一句话归纳：训练过程学习的是每一步的噪声预测函数，采样过程则从标准高斯分布开始采样，然后减去预测噪声，不断迭代生成新样本

训练和采样过程伪代码如下：

我的疑问：

正常的有监督训练都是学习一个确定的标签，但是扩散模型中同一个每个epoch中每个时间点间产生的噪声都不一样，这怎么训练？
用原来的后验分布来近似，最后不应该生成的图片大致都和训练集的差不多吗，为什么模型能生成完全没见过的图片？
前向过程不是一次采样高斯噪声就能得来吗，那反向过程中迭代用的标签都是这一个噪声吗？

模型设计

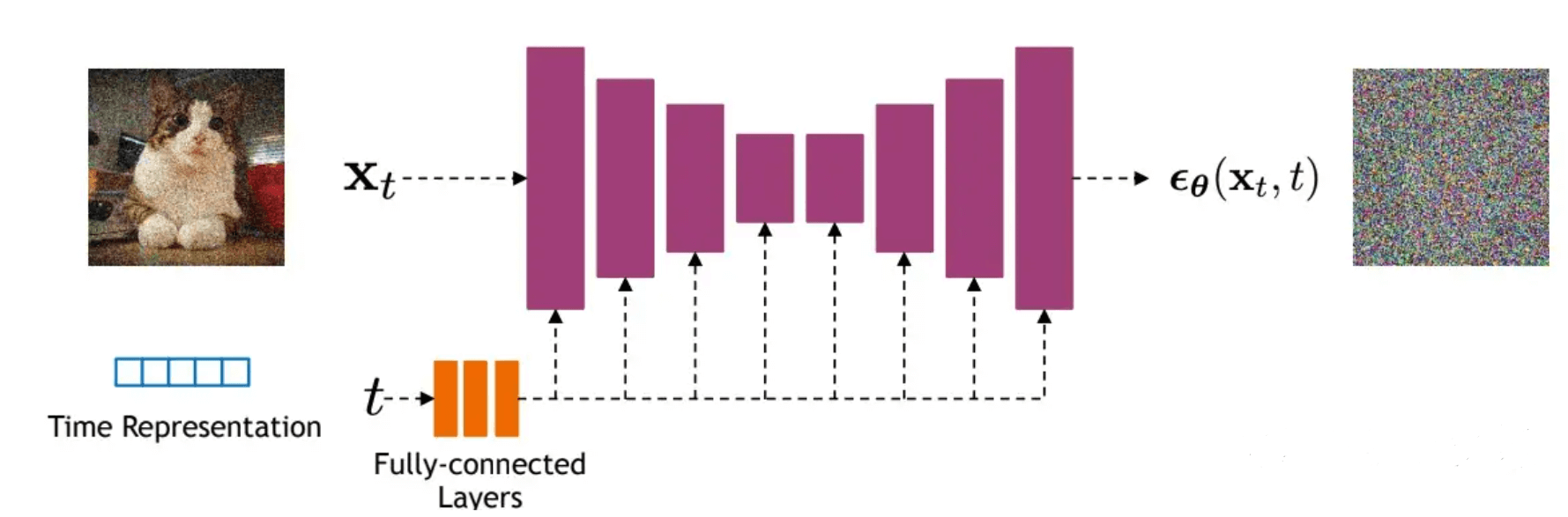
由于噪音和原始数据是同维度的，所以作者选择采用AutoEncoder架构来作为噪音预测模型。DDPM所采用的模型是一个基于residual block和attention block的U-Net模型

U-Net属于encoder-decoder架构，其中encoder分成不同的stages，每个stage都包含下采样模块来降低特征的空间大小（H和W），然后decoder和encoder相反，是将encoder压缩的特征逐渐恢复。U-Net在decoder模块中还引入了skip connection，即concat了encoder中间得到的同维度特征，这有利于网络优化。DDPM所采用的U-Net每个stage包含2个residual block，而且部分stage还加入了self-attention模块增加网络的全局建模能力。另外，扩散模型其实需要的是T个噪音预测模型，实际处理时，我们可以增加一个time embedding（类似transformer中的position embedding）来将timestep编码到网络中，从而只需要训练一个共享的U-Net模型。具体地，DDPM在各个residual block都引入了time embedding，如上图所示

LOADING